Randomization Inference en R: una mejor forma de calcular p-values en experimentos aleatorios

Bienvenidos a un nuevo artículo de la serie dedicada al libro Causal Inference: The Mixtape. En el artículo anterior vimos una introducción a la notación de outcomes potenciales y cómo esta permite expresar conceptos claves de inferencia causal.
Uno de esos conceptos claves es que la diferencia de medias simple, en presencia de un tratamiento asignado aleatoriamente, constituye un estimador insesgado del efecto causal del tratamiento (i.e. en esos casos correlación sí es causalidad).
Sin embargo, el insesgamiento (que la esperanza sea igual al efecto causal promedio) no es la única propiedad relevante de un estimador causal. También nos interesa la varianza, ya que en el mundo real observamos realizaciones particulares del proceso generador de datos que bien podrían estar muy desviadas de la esperanza1.
Para incorporar esta dimensión contamos con herramientas como los tests de medias, la regresión lineal, y el ANOVA, que relacionan la diferencia de medias observada con una varianza estimada para indicarnos qué tan seguros podemos estar de que exista una diferencia real entre las unidades tratadas y las de control (es decir, de que los procesos generadores de datos sean efectivamente distintos).
Estos métodos son muy populares y su uso está muy extendido, pero eso no significa que siempre sean la herramienta más apropiada para hacer inferencia causal con datos experimentales. Por ello, hoy hablaremos de una metodología alternativa que, en ciertas circunstancias, puede ser mejor opción para realizar tests de hipótesis sobre experimentos aleatorizados. Su nombre es Randomization Inference.
¿Por qué molestarse en aprender Randomization Inference?
Una pregunta que quizás te estés haciendo a estas alturas es porque valdría la pena invertir tiempo en aprender y aplicar esta metodología siendo que ya contamos con los tests de hipótesis tradicionales que son ampliamente usados y conocidos. Yo me estaría preguntando lo mismo.

Las razones para realizar tests de hipótesis basados en Randomization Inference (RI) pueden resumirse en las siguientes:
Al hacer inferencia causal con datos experimentales, la principal fuente de incertidumbre no es el muestreo desde una población mas grande sino que la asignación aleatoria del tratamiento combinada con la imposibilidad de conocer los contrafactuales. Los métodos tradicionales de test de hipótesis no toman esto en consideración, sino que se enfocan en la incertidumbre de muestreo. Esto es particularmente problemático si trabajamos con grandes datasets administrativos que literalmente representan “toda la data”, y puede traducirse en que subestimemos considerablemente la incertidumbre en nuestros resultados. RI aborda estos problemas al tomar en cuenta la incertidumbre proveniente de la asignación del tratamiento, por lo que es un procedimiento mas apropiado de usar en estos casos.
También existen ventajas al estar en el extremo opuesto: datos pequeños y/o con muy pocas unidades tratadas. En estos casos no resulta muy creíble apelar a las propiedades de “muestras grandes” en las que se basan los tests convencionales. En particular, podríamos sufrir de una alta vulnerabilidad a outliers y observaciones de alto leverage, lo cual se traduce en riesgo de over-rejection de la hipótesis nula. RI nos ayuda en tal situación al ser una metodología más robusta a outliers y observaciones de alto leverage, en especial cuando se combina con estadísticos de ranking o de cuantiles (los cuales se explicarán en detalle más abajo).
Finalmente, aún si no existe ningún problema particular con los tests tradicionales, RI nos entrega mucha más libertad respecto de los estimadores o estadísticos a usar. Mientras que al hacer un test de hipótesis estándar estamos restringidos a aquellos estimadores para los cuales se ha podido estimar la varianza o se ha construido el test de forma analítica, RI nos abre las puertas para usar cualquier estadístico escalar que pueda obtenerse a partir de un dataset, sin siquiera obligarnos a asumir una función de distribución para el estimador. Algunos ejemplos de estadísticos útiles que podemos usar son los estadísticos de cuantiles (por ejemplo, la mediana), los estadísticos en base a rankings, o el estadístico KS (Kolmogorov-Smirnov) que mide diferencias en las distribuciones de los outcomes.
Y como bonus, hacer Randomization Inference es cool, en el sentido de que en el mundo de la inferencia causal existe una preferencia estética por las metodologías de “placebo” y RI puede considerarse como una de ellas. Este tipo de metodologías se caracterizan por simular tratamientos falsos en datos reales y chequear que no encontremos un efecto relevante asociado a esos tratamientos falsos, para así estar mas seguros de que nuestras conclusiones sobre el tratamiento verdadero son válidas2. Más abajo veremos que Randomization Inference consiste en algo muy similar a esto.
Randomization Inference paso a paso en R
Para pasar a explicar la metodología en sí, recordemos primero el objetivo y contexto en el cual aplicaríamos este procedimiento. Estamos analizando datos provenientes de un experimento aleatorizado y tenemos:
Un conjunto de observaciones que fueron asignadas aleatoriamente a grupos de tratamiento y control.
Una variable de resultados (\(Y\)).
Y queremos determinar si el tratamiento tiene algún efecto sobre dicha variable de resultados.
Ya que casi siempre existirán diferencias entre el grupo tratado y el grupo de control (simplemente por la variabilidad natural del proceso generador de datos), es necesario realizar algún test de hipótesis para determinar si las diferencias observadas son lo suficientemente grandes como para ser consideradas evidencia de un efecto causal.
Estando en esta situación, podemos realizar un test de hipóteis con Randomization Inference mediante aplicar los siguientes pasos.
Paso 1: escoger una hipótesis nula “sharp”
En un test de hipótesis estándar tenemos una hipótesis nula que afirma algo respecto a un parámetro poblacional, por ejemplo, \(\beta_1=0\) donde \(\beta_1\) es el coeficiente asociado a la variable de tratamiento \(D\). Lo que esta hipótesis nula plantea es que el efecto promedio del tratamiento es 0, pero no dice nada acerca de los efectos del tratamiento para cada unidad (\(\delta_i\)).
En cambio, al aplicar RI utilizamos una hipótesis nula sharp, es decir, una nula que afirma algo sobre los efectos en cada una de las unidades.
La más usada y conocida es la sharp null de Fischer:
\[ \delta_i=0 \]
Que nos plantea que el tratamiento tiene efecto cero para todas las unidades analizadas.
Para efectos de simplicidad, en este post se usará la sharp null de Fischer, pero notar que podríamos perfectamente testear hipótesis alternativas tales como \(\delta_i=1\), \(\delta_i=2\), etc. Incluso podríamos testear hipótesis en las que diferentes grupos o unidades tengan valores de \(\delta_i\) distintos. Lo único que se requiere es tener una hipótesis que plantee algo respecto de cada uno de los \(\delta_i\).
¿Qué ganamos con usar una nula de este tipo? Pues que nos permite completar las columnas de Potential Outcomes en nuestro dataset.
Los datos que observamos normalmente tienen esta estructura:
library(tidyverse)
library(magrittr)
library(causaldata)
ri <- causaldata::ri %>%
mutate(id_unit = row_number(),
y0 = as.numeric(y0),
y1 = as.numeric(y1))
ri## # A tibble: 8 x 6
## name d y y0 y1 id_unit
## <chr> <dbl> <dbl> <dbl> <dbl> <int>
## 1 Andy 1 10 NA 10 1
## 2 Ben 1 5 NA 5 2
## 3 Chad 1 16 NA 16 3
## 4 Daniel 1 3 NA 3 4
## 5 Edith 0 5 5 NA 5
## 6 Frank 0 7 7 NA 6
## 7 George 0 8 8 NA 7
## 8 Hank 0 10 10 NA 8Para todas las unidades observamos \(D_i\) e \(Y_i\), pero solo uno de los outcomes potenciales (\(Y_i^0\) o \(Y_i^1\)). Apalancándonos en la sharp null, podemos completar las columnas y0 e y1 en base a \(Y_i=Y_i^0=Y_i^1\)
ri_fischer_null <- ri %>%
mutate(y0 = y,
y1 = y)
ri_fischer_null## # A tibble: 8 x 6
## name d y y0 y1 id_unit
## <chr> <dbl> <dbl> <dbl> <dbl> <int>
## 1 Andy 1 10 10 10 1
## 2 Ben 1 5 5 5 2
## 3 Chad 1 16 16 16 3
## 4 Daniel 1 3 3 3 4
## 5 Edith 0 5 5 5 5
## 6 Frank 0 7 7 7 6
## 7 George 0 8 8 8 7
## 8 Hank 0 10 10 10 8Como estamos asumiendo que el tratamiento tiene un efecto igual a cero para todas las unidades, ambos outcomes potenciales son iguales al outcome observado.
Por supuesto, no estamos afirmando que esto sea así realmente, simplemente queremos descubrir qué tan improbable es haber observado las diferencias entre grupos que estamos observando bajo el supuesto de esta sharp null.
Paso 2: escoger un estadístico de test
Para realizar un test de hipótesis necesitamos no solo una hipótesis nula sino que también un estadístico. En un test de hipótesis tradicional, sería necesario que este estadístico cuente con un estimador para su varianza, pero al aplicar randomization inference podemos usar literalmente cualquier estadístico escalar que pueda obtenerse a partir de un vector de asignaciones de tratamiento (\(D\)) y de un vector de outcomes (\(Y\)).
Uno de los estadísticos más simples que podemos usar es la diferencia simple de medias (SDO) entre ambos grupos.
# Funcion que define el estadístico: recibe como input un dataframe con
# las columnas `y` (outcome) y `d` (asignacion de tratamiento), y retorna
# un valor escalar
sdo <- function(data) {
data %>%
summarise(te1 = mean(y[d == 1]),
te0 = mean(y[d == 0]),
sdo = te1 - te0) %>%
pull(sdo)
}
sdo(ri_fischer_null)## [1] 1Sin embargo, nada impide usar otros estadísticos de test. Esta libertad es de hecho una de las principales ventajas de aplicar Randomization Inference.
Algunos ejemplos de estadísticos alternativos que podríamos usar son:
Estadísticos de quantiles, por ejemplo la diferencia de medianas entre grupos (o cualquier otro percentil). Útiles si tenemos outliers u observaciones de alto leverage.
Estadísticos de ranking, que convierten la variable de outcomes (\(Y\)) en valores de ranking (1 para el outcome más bajo, 2 para el segundo más bajo, etc) y luego computan una métrica en base a esos rankings (por ejemplo, diferencia de medias o de medianas).
Estadístico KS (Kolmogorov-Smirnov), que permite identificar diferencias en las distribuciones de outcomes mediante medir la distancia máxima entre ambas funciones de distribución acumuladas. Este estadístico nos permitiría, por ejemplo, detectar el efecto de un tratamiento que no afecte la media de \(Y\), pero sí su varianza o dispersión.
Para mantener la simplicidad, a continuación se usará el SDO como estadístico de test, pero más abajo mostraré ejemplos de código utilizando el estadístico KS.
Paso 3: simular distintas asignaciones de tratamiento y obtener la distribución del estadístico
El siguiente consiste en obtener la distribución de valores que podría tomar el estadístico del test bajo la sharp null.
Para esto:
Realizaremos permutaciones en el vector \(D\) mediante el mismo proceso aleatorio que se utilizó para obtener las asignaciones de tratamiento originales en primer lugar. Por ejemplo, si para asignar el tratamiento se usó un proceso equivalente a lanzar una moneda al aire para cada observación (\(B(n, 0.5)\)), entonces cada una de las permutaciones deben generarse con el mismo proceso.3
En nuestro ejemplo, el proceso consiste en sortear 4 asignaciones de tratamiento para un total de 8 observaciones, lo cual produce 70 permutaciones posibles en total. El siguiente código obtiene tales permutaciones:
perms <- t(combn(ri_fischer_null$id_unit, 4)) %>% asplit(1) perms_df <- tibble(treated_units = perms) %>% transmute(id_perm = row_number(), treated_units = map(treated_units, unlist)) ri_permuted <- crossing(perms_df, ri_fischer_null) %>% mutate(d = map2_dbl(id_unit, treated_units, ~.x %in% .y)) ri_permuted## # A tibble: 560 x 8 ## id_perm treated_units name d y y0 y1 id_unit ## <int> <list> <chr> <dbl> <dbl> <dbl> <dbl> <int> ## 1 1 <int [4]> Andy 1 10 10 10 1 ## 2 1 <int [4]> Ben 1 5 5 5 2 ## 3 1 <int [4]> Chad 1 16 16 16 3 ## 4 1 <int [4]> Daniel 1 3 3 3 4 ## 5 1 <int [4]> Edith 0 5 5 5 5 ## 6 1 <int [4]> Frank 0 7 7 7 6 ## 7 1 <int [4]> George 0 8 8 8 7 ## 8 1 <int [4]> Hank 0 10 10 10 8 ## 9 2 <int [4]> Andy 1 10 10 10 1 ## 10 2 <int [4]> Ben 1 5 5 5 2 ## # ... with 550 more rowsri_permuted %>% pull(id_perm) %>% n_distinct()## [1] 70Para cada permutación, simulamos los valores de \(Y\) en base a la hipótesis nula escogida previamente. Para la sharp null de Fischer literalmente no hay que hacer nada, ya que al plantear esta que \(Y_i=Y_i^0=Y_i^1\), el vector \(Y\) se mantiene constante en cada permutación de \(D\) (sin embargo, si nuestra sharp null fuera algo como \(\delta_i=1\) entonces sí habría que cambiar los valores de \(Y\) con cada permutación).
Calcularemos el valor del estadístico del test (el SDO en nuestro caso) para cada una de estas permutaciones y guardamos su valor.
perms_stats <- ri_permuted %>% group_by(id_perm) %>% summarise(te1 = mean(y[d == 1]), te0 = mean(y[d == 0]), sdo = te1 - te0) perms_stats %>% select(id_perm, sdo)## # A tibble: 70 x 2 ## id_perm sdo ## <int> <dbl> ## 1 1 1 ## 2 2 2 ## 3 3 3 ## 4 4 3.5 ## 5 5 4.5 ## 6 6 -4.5 ## 7 7 -3.5 ## 8 8 -3 ## 9 9 -2 ## 10 10 -2.5 ## # ... with 60 more rowsListo! Los valores del estadístico obtenidos en (3) nos indican la distribución de este bajo la sharp null.
ggplot(perms_stats, aes(sdo)) + geom_histogram() + labs(x = "Estadístico del test (SDO)")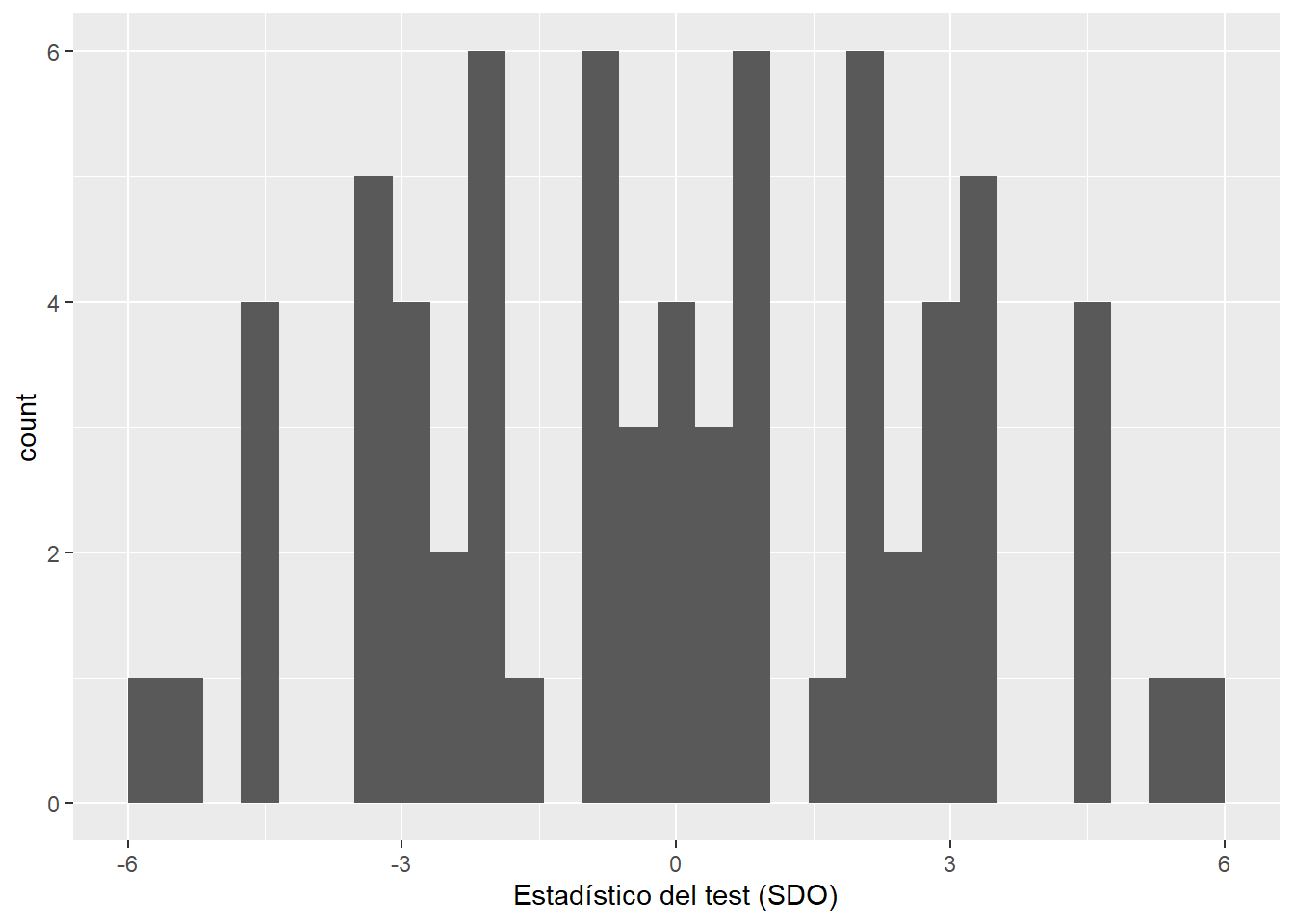
¿Cuántas permutaciones se deben realizar? Lo ideal sería agotar todas permutaciones posibles para conseguir una representación exacta de la distribución del estadístico de test bajo la sharp null. Sin embargo, esto solo es factible en datasets muy pequeños: incluso con un dataset de 2000 observaciones ya se vuelve computacionalmente prohibitivo obtener todas las combinaciones posibles del vector \(D\).
La alternativa en ese caso es conformarnos con hacer las permutaciones suficientes para obtener una aproximación razonable a la distribución del estadístico4.
Paso 4: comparar el estadístico “real” con la distribución simulada para obtener el p-value
Luego de haber obtenido la distribución (exacta o aproximada) del estadístico bajo la sharp null, procedemos a ubicar el estadístico “verdadero” (aquel correspondiente los valores reales de \(D\) e \(Y\)) dentro de esa distribución.
Notar que si queremos realizar un test de dos colas (lo más usual) debemos aplicar valor absoluto a la distribución de estadísticos (que es de hecho lo que haremos en este ejemplo).
true_statistic <- perms_stats %>%
filter(id_perm == 1) %>%
pull(sdo)
ggplot(perms_stats,
# Aplicamos valor absoluto porque haremos un test de 2 colas
aes(abs(sdo))) +
geom_histogram() +
labs(x = "Valor absoluto del estadístico del test (SDO)",
y = "count") +
geom_vline(xintercept = true_statistic, colour = "red", size = 2) +
annotate(geom = "label",
x = true_statistic,
y = 10,
label = "Estadístico 'verdadero'",
colour = "red") +
annotate("segment", x = true_statistic+1, xend = true_statistic+3, y = 9, yend =9,
colour = "purple", size = 2, arrow = arrow()) +
annotate(geom = "label",
x = true_statistic+2,
y = 10,
label = "Estadísticos más extremos",
colour = "purple")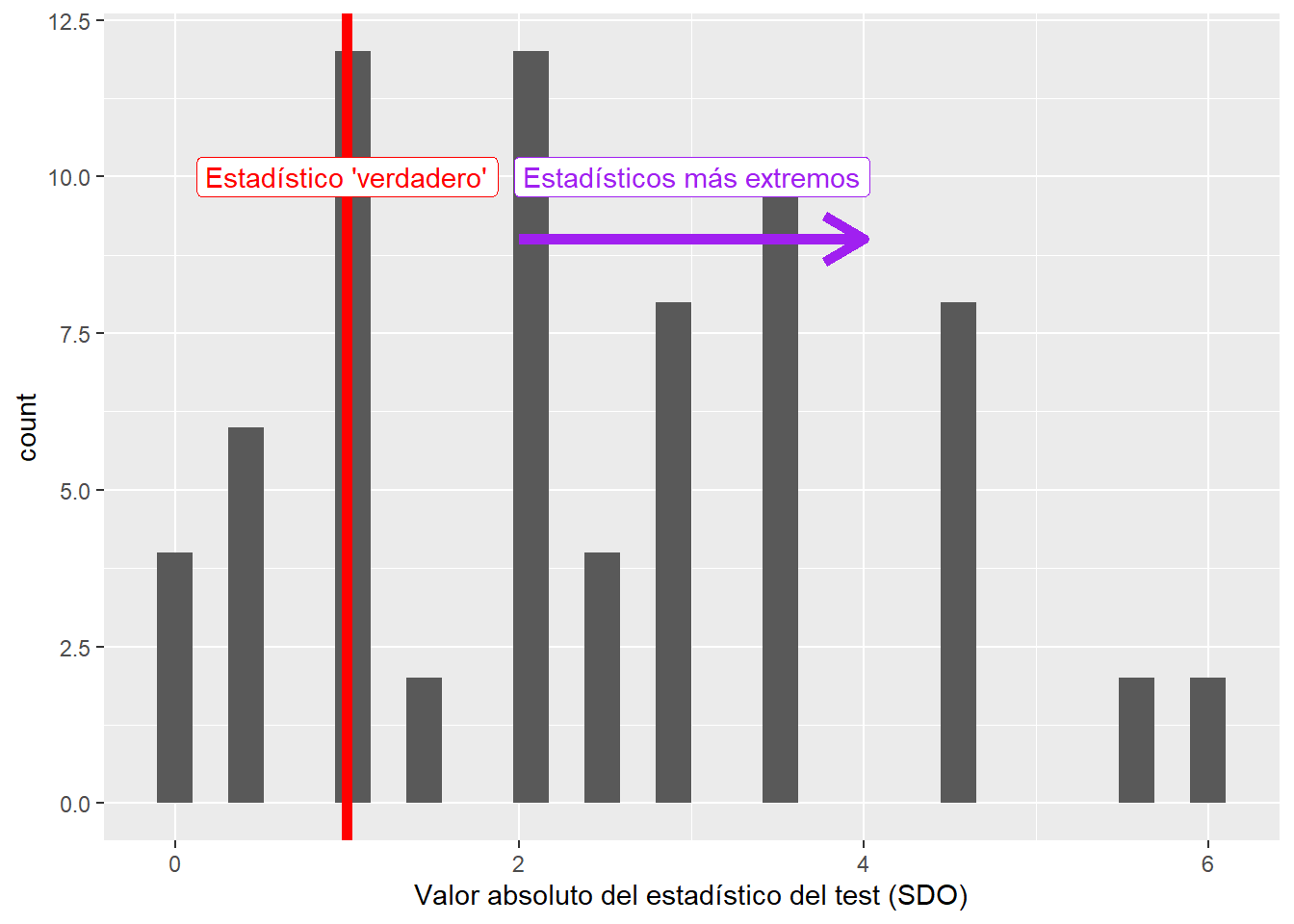
Habiendo hecho esto procedemos a calcular el p-value (que es lo que hemos estado buscando desde un comienzo).
Este p-value se calcula en dos pasos:
- Se crea un ranking descendiente de los estadísticos de test obtenidos en las permutaciones (el con mayor valor tiene ranking 1 y el con menor valor tiene ranking N). Para los estadísticos “empatados” en un mismo valor, su ranking corresponde el máximo de los rankings originales de los estadísticos que comparten tal valor (por ejemplo, si tres estadísticos son iguales y tienen rankings 2, 3, y 4, todos ellos quedan con ranking igual a 4).
perms_ranked <- perms_stats %>%
# Igual que antes, se aplica valor absoluto para tener un test de dos colas
mutate(abs_sdo = abs(sdo)) %>%
select(id_perm, abs_sdo) %>%
arrange(desc(abs_sdo)) %>%
mutate(rank = row_number(desc(abs_sdo))) %>%
group_by(abs_sdo) %>%
mutate(new_rank = max(rank))
perms_ranked## # A tibble: 70 x 4
## # Groups: abs_sdo [11]
## id_perm abs_sdo rank new_rank
## <int> <dbl> <int> <int>
## 1 25 6 1 2
## 2 46 6 2 2
## 3 24 5.5 3 4
## 4 47 5.5 4 4
## 5 5 4.5 5 12
## 6 6 4.5 6 12
## 7 22 4.5 7 12
## 8 23 4.5 8 12
## 9 48 4.5 9 12
## 10 49 4.5 10 12
## # ... with 60 more rows- Se calcula el ratio entre el ranking del estadístico verdadero y el total de permutaciones obtenidas (N).
n <- nrow(perms_ranked)
p_value <-
perms_ranked %>%
filter(id_perm == 1) %>%
pull(new_rank)/n
p_value## [1] 0.8571429En nuestro caso, el p-value obtenido es de 0.86, lo que implica que no podemos rechazar la sharp null con un 5% de significancia (ni con ningún nivel de significancia convencional 😅). Dicho de otra forma, el valor de SDO observado no es un valor improbable de observar si asumimos que el tratamiento no tuvo efecto en ninguna unidad y que la única fuente de variabilidad en el estadístico es la asignación aleatoria de \(D\).
Haciéndolo más fácil con el paquete ri2 🤗
El código en R mostrado arriba tenía como fin explicar en qué consiste cada paso del procedimiento. Sin embargo, no es muy conciso y adaptarlo para otros datasets puede resultar un poco tedioso. Por ello, para aplicar Randomization Inference en nuestros propios datos es recomendable usar paquetes de R diseñados para este fin, tales como ri2.
library(ri2)Algo que no cambia respecto al código “manual” es que siempre debemos suministrar 1) un estadístico de test, 2) una hipótesis nula sharp, y 3) un procedimiento de randomización. E igual que antes, el procedimiento de randomización indicado en el código debe ser idéntico al que se utilizó para asignar el tratamiento en primer lugar.
Para declarar el procedimiento de randomización se usa la función ri2::declare_ra. En este caso (igual que en el ejemplo de antes) estamos declarando la asignación aleatoria de 4 unidades tratadas (m = 4) dentro de una muestra de 8 unidades (N = 8).
declaration <- declare_ra(N = 8, m = 4)
declaration## Random assignment procedure: Complete random assignment
## Number of units: 8
## Number of treatment arms: 2
## The possible treatment categories are 0 and 1.
## The number of possible random assignments is 70.
## The probabilities of assignment are constant across units:
## prob_0 prob_1
## 0.5 0.5El output de declare_ra se guarda en un objeto de R, que luego podremos pasar a la función ri2::conduct_ri, que es la que realiza el procedimiento de Randomization Inference en sí mismo.
Para declarar el estadístico del test tenemos 2 opciones.
Una es hacerlo mediante el argumento formula de conduct_ri. Si nuestro estadístico es simplemente la diferencia de medias entre tratados y controles, la fórmula será algo como y ~ d (con y como variable de outcome y d como variable de asignación de tratamiento).
Alternativamente, podemos especificar el estadístico mediante el argumento test_function (también de conduct_ri), el cual admite cualquier función de R capaz de recibir un dataframe y retornar un escalar (i.e., el valor del estadístico de test).
# Declarando la `test_function`
sdo <- function(data) {
data %>%
summarise(te1 = mean(y[d == 1], na.rm=TRUE),
te0 = mean(y[d == 0], na.rm=TRUE),
sdo = te1 - te0) %>%
pull(sdo)
}La hipótesis nula sharp se especifica mediante el argumento sharp_hypothesis de conduct_ri. Su valor por defecto es 0, así que si vamos a usar la sharp null de Fischer podemos omitirlo.
Otro detalle importante es que debemos indicar los nombres de las columnas correspondientes al outcome y al tratamiento en el dataset, usando los argumentos assignment y outcome. Y también hay que pasar el dataset en sí mismo con el argumento data.
Finalmente, ejecutamos la función conduct_ri con todos los argumentos necesarios e inspeccionamos los resultados con la función summary.
ri2_out <- conduct_ri(
test_function = sdo,
assignment = "d",
outcome = "y",
declaration = declaration,
sharp_hypothesis = 0,
data = ri
)
summary(ri2_out)## term estimate two_tailed_p_value
## 1 Custom Test Statistic 1 0.8571429Como vemos, el p-value retornado por conduct_ri es idéntico al que obtuvimos ejecutando el código de la sección anterior, pero con la ventaja de que el código de ri2 es mucho más conciso y legible.
Otra ventaja de ri2::conduct_ri es que su output puede ser graficado directamente con la función plot().
plot(ri2_out)## Warning: It is deprecated to specify `guide = FALSE` to remove a guide. Please
## use `guide = "none"` instead.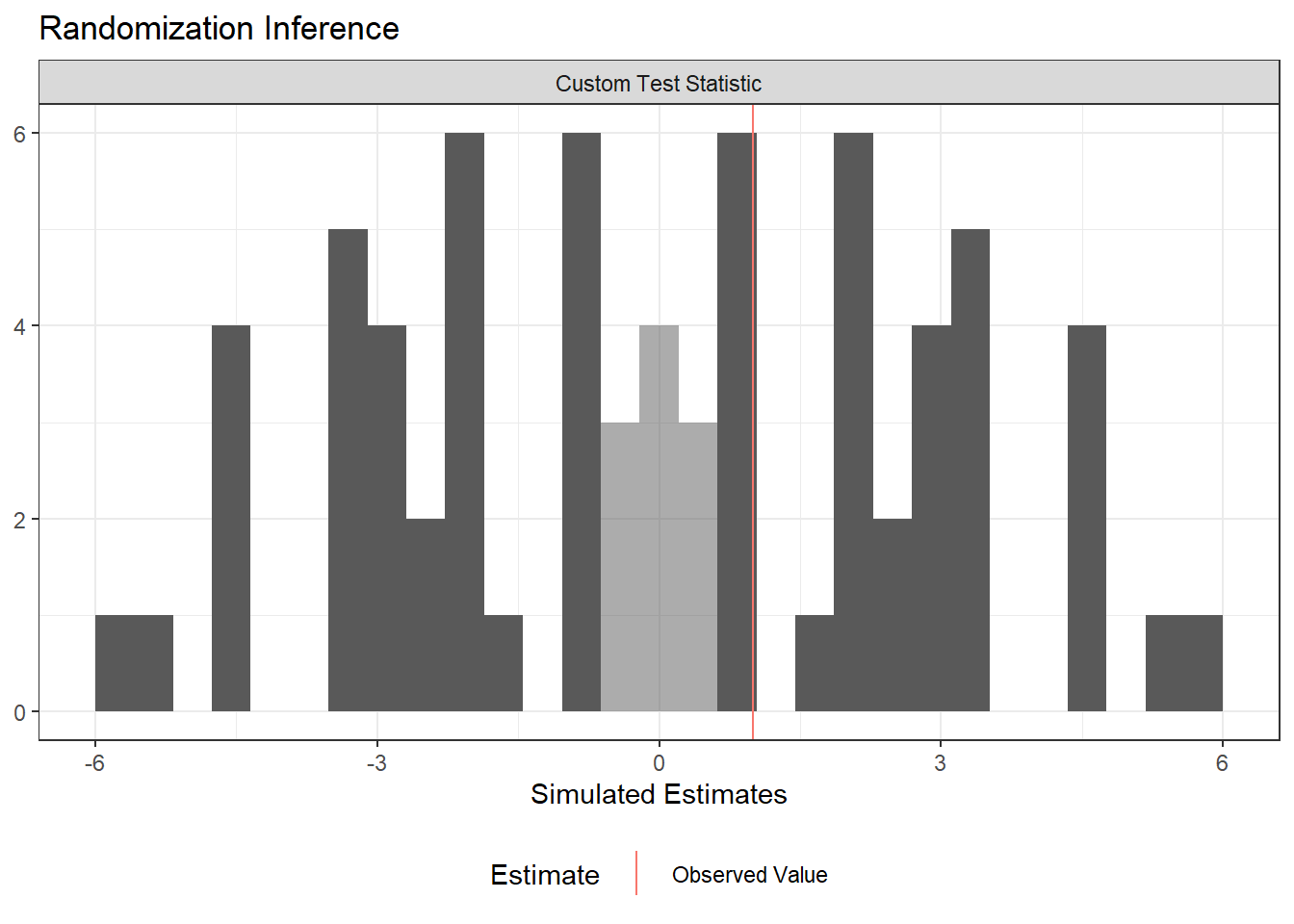
Este gráfico es incluso mejor que el creado a mano en la sección anterior porque destaca automáticamente los estadísticos que son tan o más extremos que el estadístico simulado, y representa apropiadamente los tests de dos colas sin tener que transformar los estadísticos a valor absoluto ✨.
Además, dado que el output de plot(ri2_out) es un objeto de ggplot2, podemos personalizar el gráfico usando las funciones de ggplot2 que ya conocemos. Por ejemplo, podemos aplicarle un tema de ggthemes:
plot(ri2_out) +
ggthemes::theme_stata()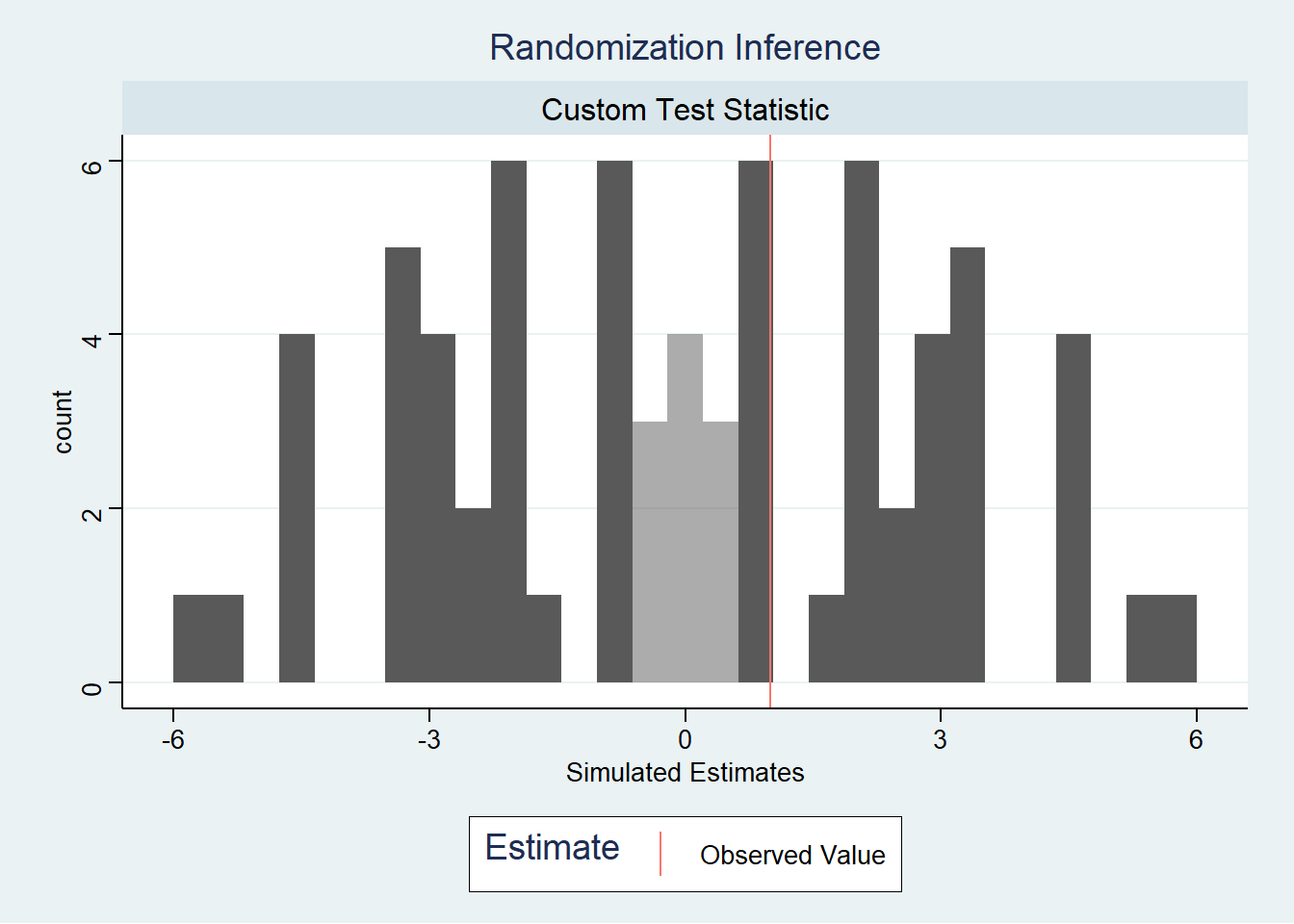
Si queremos inspeccionar manualmente la data de las simulaciones, es posible hacerlo extrayendo el dataframe sims_df desde el output de ri2::conduct_ri. Este dataframe tendrá tantas filas como permutaciones de \(D\) se hayan efectuado.
ri2_out[["sims_df"]] %>% head()## est_sim est_obs term
## 1 -1.0 1 Custom Test Statistic
## 2 -2.0 1 Custom Test Statistic
## 3 -3.0 1 Custom Test Statistic
## 4 -3.5 1 Custom Test Statistic
## 5 -4.5 1 Custom Test Statistic
## 6 4.5 1 Custom Test StatisticVale la pena mencionar además que conduct_ri tiene un argumento sims que indica la cantidad de permutaciones a realizar para obtener el p-value. Por defecto su valor es 1000, pero podemos querer incrementarlo en caso de que deseemos obtener una aproximación más precisa.
Bonus: usando el estadístico KS para medir diferencias en distribuciones de outcomes
Una de las ventajas de RI mencionadas al comienzo de este post era la posibilidad de utilizar estadísticos alternativos, siendo el único requisito sobre estos el que correspondan a valores escalares obtenidos a partir de \(D\) e \(Y\).
Uno de los estadísticos “alternativos” más interesantes (en mi opinión) es el estadístico KS (Kolmogorov-Smirnov) que mide la diferencia máxima entre dos funciones de distribución acumuladas empíricas (en este caso, entre la de las unidades tratadas \(\hat{F_T}\) y la de las unidades de control \(\hat{F_C}\)):
\[ T_{KS}=\max|\hat{F_T}(Y_i) - \hat{F_C}(Y_i)| \]
Lo cual se puede apreciar visualmente en el siguiente gráfico de ejemplo, donde el valor del estadístico corresponde al largo de la línea roja punteada.

Ejemplo de estadístico KS con 2 funciones de distribución acumuladas. Fuente: StackExchange
¿Por qué querríamos usar el estadístico KS en vez de algo más familiar, como la diferencia de medias?
Porque puede haber casos en que el tratamiento afecte la distribución de los outcomes, pero sin generar cambios importantes en la media, por ejemplo aumentando la dispersión, o generando una distribución bimodal. He aquí un ejemplo (tomando del Mixtape) con datos simulados:
tb <- tibble(
d = c(rep(0, 20), rep(1, 20)),
y = c(0.22, -0.87, -2.39, -1.79, 0.37, -1.54,
1.28, -0.31, -0.74, 1.72,
0.38, -0.17, -0.62, -1.10, 0.30,
0.15, 2.30, 0.19, -0.50, -0.9,
-5.13, -2.19, 2.43, -3.83, 0.5,
-3.25, 4.32, 1.63, 5.18, -0.43,
7.11, 4.87, -3.10, -5.81, 3.76,
6.31, 2.58, 0.07, 5.76, 3.50)
)
kdensity_d1 <- tb %>%
filter(d == 1) %>%
pull(y)
kdensity_d1 <- density(kdensity_d1)
kdensity_d0 <- tb %>%
filter(d == 0) %>%
pull(y)
kdensity_d0 <- density(kdensity_d0)
kdensity_d0 <- tibble(x = kdensity_d0$x, y = kdensity_d0$y, d = 0)
kdensity_d1 <- tibble(x = kdensity_d1$x, y = kdensity_d1$y, d = 1)
kdensity <- full_join(kdensity_d1, kdensity_d0,
by = c("x", "y", "d"))
kdensity$d <- as_factor(kdensity$d)
ggplot(kdensity)+
geom_point(size = 0.3, aes(x,y, color = d))+
xlim(-7, 8)+
scale_color_discrete(labels = c("Control", "Treatment"))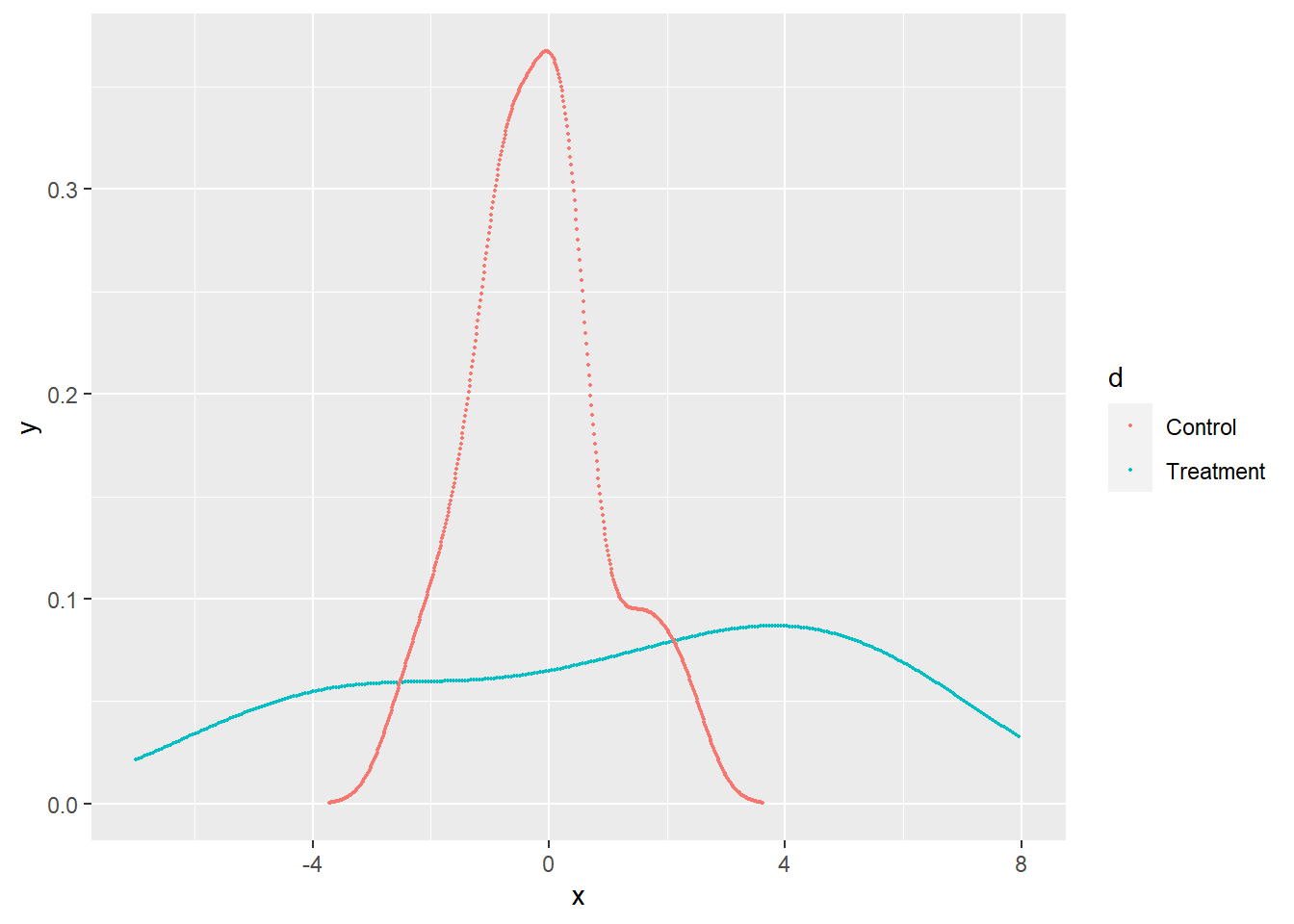
En el ejemplo de arriba, si hacemos randomization inference usando el SDO como estadístico no podemos descartar la sharp null de que el efecto del tratamiento es cero para todas las unidades, a pesar de que claramente las distribuciones son muy distintas.
set.seed(1989)
conduct_ri(
test_function = sdo,
assignment = "d",
outcome = "y",
declaration = declare_ra(N = 40, m = 20),
sharp_hypothesis = 0,
data = tb,
sims = 10000
)## term estimate two_tailed_p_value
## 1 Custom Test Statistic 1.415 0.1361Veamos qué resultado obtenemos al usar el estadístico KS en vez del SDO:
# Declarando la función que obtiene el estadístico KS a partir de un dataframe
ks_statistic <- function(data) {
control <- data[data$d == 0, ]$y
treated <- data[data$d == 1, ]$y
cdf1 <- ecdf(control)
cdf2 <- ecdf(treated)
minMax <- seq(min(control, treated),
max(control, treated),
length.out=length(c(control, treated)))
x0 <-
minMax[which(abs(cdf1(minMax) - cdf2(minMax)) == max(abs(cdf1(minMax) - cdf2(minMax))))]
y0 <- cdf1(x0)
y1 <- cdf2(x0)
diff <- unique(abs(y0 - y1))
diff
}
# obteniendo el p-value con randomization inference
set.seed(1989)
ri_ks <-
conduct_ri(
test_function = ks_statistic,
assignment = "d",
outcome = "y",
declaration = declare_ra(N = 40, m = 20),
sharp_hypothesis = 0,
data = tb,
sims = 10000
)
ri_ks## term estimate two_tailed_p_value
## 1 Custom Test Statistic 0.45 0.0227El estadístico KS sí permite rechazar la nula de efecto 0 a un nivel de significancia del 5%5.
En la siguiente figura podemos visualizar el estadístico KS correspondiente al vector \(D\) verdadero, junto con las CDF empíricas de los grupos de tratamiento y control.
tb2 <- tb %>%
group_by(d) %>%
arrange(y) %>%
mutate(rn = row_number()) %>%
ungroup()
cdf1 <- ecdf(tb2[tb2$d == 0, ]$y)
cdf2 <- ecdf(tb2[tb2$d == 1, ]$y)
minMax <- seq(min(tb2$y),
max(tb2$y),
length.out=length(tb2$y))
x0 <-
minMax[which(abs(cdf1(minMax) - cdf2(minMax)) == max(abs(cdf1(minMax) - cdf2(minMax))) )]
y0 <- cdf1(x0)
y1 <- cdf2(x0)
ggplot(tb2) +
geom_step(aes(x=y, y=rn, color=factor(d)),
size = 1.5, stat="ecdf") +
labs(y = "Densidad") +
geom_segment(aes(x = x0[1], y = y0[1], xend = x0[1], yend = y1[1]),
linetype = "dashed", color = "red", size = 1) +
geom_point(aes(x = x0[1] , y= y0[1]), color="red", size=4) +
geom_point(aes(x = x0[1] , y= y1[1]), color="red", size=4)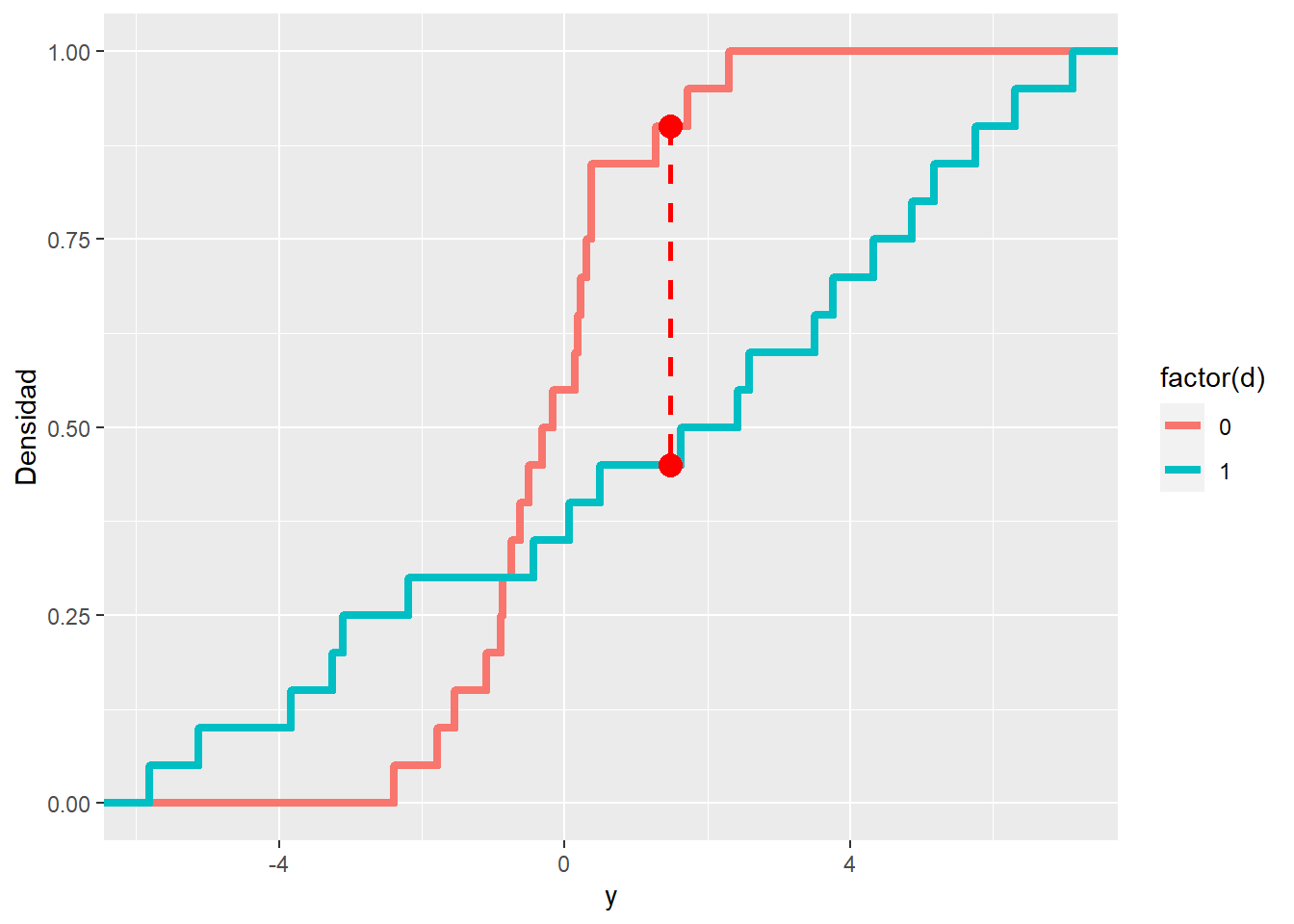
Consideraciones y referencias adicionales 🔍📚
Para concluir, quiero comentar algunos detalles adicionales y consideraciones respecto a esta metodología:
Para obtener intervalos de confianza con RI podemos crear un vector con un rango de valores posibles para el estadístico del test (ej, 0.1, 0.2, 0.3, etc) y usar cada uno de ellos como sharp null mediante iteración. El intervalo de confianza estará compuesto de todos aquellos valores para los cuales la sharp null no se rechace.
En el Mixtape se nos advierte que randomization inference presenta cierto sesgo en contra de los efectos pequeños cuando se usa junto a la sharp null de Fischer. Esto debido a que solo treatment effects relativamente grandes permitirán rechazar esta nula a niveles convencionales de significancia. Por ende, si el efecto esperado de nuestro tratamiento es pequeño, nos conviene agregar covariates que expliquen la variable de outcome (esto se puede hacer con el argumento
formuladeri2::conduct_ri), o directamente no usar RI.Otra crítica que existe hacia esta metodología es que, según Andrew Gelman de Columbia University, la sharp null representa una hipótesis “poco interesante y académica”, ya que la idea de un efecto constante para todas las unidades sería demasiado restrictiva. En respuesta a eso, Xinran Li de UIUC plantea la idea de generalizar el procedimiento para obtener cuantiles de efectos individuales, y así llegar a conclusiones tales como “el X% de las unidades experimenta un efecto causal superior a Y”.
Existe un paquete alternativo a
ri2para realizar Randomization Inference en R, denominadoritest. Es un port de un comando de STATA con el mismo nombre, por lo que puede ser de interés para quienes estén más familiarizados con STATA.
Finalmente, compartirles un par de referencias en caso de que deseen profundizar más.
La vignette del paquete
ri2contiene ejemplos de cómo usar sus funciones para diseños experimentales más complejos, tales como cuando se prueban varios tratamientos al mismo tiempo (multi-arm design), se desea evaluar interacciones con covariables, o se hace randomización con clustering o blocking por grupos.Este apunte de Matthew Blackwell resume muy bien los conceptos de randomization inference, por lo que resulta buen material de consulta o repaso (de hecho me apoye en él para escribir este artículo, junto con el capítulo 4 de Causal Inference: The Mixtape).
El capítulo 5 de Causal Inference for Statistics, Social, and Biomedical Sciences de Imbens y Rubin (2015) entra en más detalle en varios tópicos de Randomization Inference, en especial en lo que respecta a los estadísticos de test.
Tu feedback es bienvenido. Si tienes comentarios sobre este artículo puedes enviármelos por correo.
Por ejemplo, dos monedas tienen la misma esperanza de arrojar cara o sello al ser lanzadas, pero si lanzamos cada una 5 veces, es muy probable que el número de caras y sellos difiera entre ellas, simplemente debido a la fluctuación aleatoria o varianza propia de este proceso generador de datos.↩︎
Algunas de las metodologías de inferencia causal que se apalancan mucho en tests de placebo son regresión discontinua y diferencias en diferencias. En artículos posteriores se las discutirá en más detalle.↩︎
O si se usó clustering o blocking por grupos al hacer la randomización, también debe usarse al obtener las permutaciones.↩︎
Como referencia, la función
ri2::conduct_ri, que es una de las implementaciones de Randomization Inference que existen R, realiza 1000 simulaciones/permutaciones por defecto.↩︎Por supuesto, es mala idea repetir el test con múltiples estadísticos hasta encontrar uno que permita rechazar la nula, ya que eso constituiría p-hacking. El estadístico a usar debería, creo, ser parte del diseño del experimento.↩︎